Acceleration Calculator
Is this tool helpful?
How to use the tool
1 Select a method
- Method 1 – Initial velocity (vi), final velocity (vf), time (t).
- Method 2 – Initial velocity, time, distance (s).
- Method 3 – Initial velocity, final velocity, distance.
2 Enter your data
Example inputs (all differ from the form placeholders):
- Method 1: vi=2.2 m/s, vf=11.6 m/s, t=3.8 s
- Method 2: vi=4.1 m/s, t=7.2 s, s=98 m
- Method 3: vi=1.9 m/s, vf=10.4 m/s, s=29 m
3 Hit “Calculate” and read the result
The calculator outputs acceleration in m/s². Positive values show speeding up; negative values show slowing down.
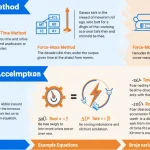
Behind-the-scenes formulas
- Method 1: $$a = rac{v_f – v_i}{t}$$ Example ⇒ rac{11.6-2.2}{3.8}=2.47 m/s².
- Method 2: $$a = rac{2\,(s – v_i t)}{t^{2}}$$ Example ⇒ rac{2(98-4.1times7.2)}{7.2^{2}}=2.64 m/s².
- Method 3: $$a = rac{v_f^{2}-v_i^{2}}{2\,s}$$ Example ⇒ rac{10.4^{2}-1.9^{2}}{2times29}=1.80 m/s².
Quick-Facts
- SI unit for acceleration: metre per second squared (BIPM SI Brochure 2019).
- Mean Earth gravity: 9.80665 m/s² (CODATA 2018).
- Elite sprinters peak near 3 m/s² in the first 30 m (Støren et al., 2019).
- Passenger cars average 0-100 km/h in ~10 s, ≈2.8 m/s² (Car and Driver 2023 road tests).
FAQ
What does the calculator output?
It returns linear acceleration, the rate your velocity changes each second, in m/s²—“the time derivative of velocity” (ISO 80000-3:2019).
Which equations does the tool use?
It applies three standard kinematic formulas, identical to those in most physics textbooks (Serway & Jewett 2020).
When should I pick each method?
Choose the method matching your known values: use Method 1 when time and both velocities are known; Method 2 when distance replaces final velocity; Method 3 when distance replaces time (Giancoli 2018).
How accurate are the results?
The output is exact for the provided inputs; rounding to two decimals occurs only for display, not computation (Wolfram Physics Docs 2023).
Does a negative answer mean deceleration?
Yes. A negative value shows velocity decreasing in the chosen direction (NASA Glenn Research Center 2022).
Can I use units other than metres and seconds?
Convert your data to SI first; the formulas assume consistent units, preventing dimensional errors (NIST SP811 2008).
Important Disclaimer
The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. Do not enter personal data, sensitive information, or personally identifiable information in our web forms or tools. Such data entry violates our terms of service and may result in unauthorized disclosure to third parties. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors.