Find acceleration fast: type the object’s final speed and the time taken; the calculator simply divides the two. Earth’s standard gravity is 9.80665 m/s², a handy benchmark (BIPM, 2019).
Acceleration Calculator
★ Add to Home Screen
×
Follow these steps:
Tap the Share button at the bottom of the browser
Scroll down and tap “Add to Home Screen”
Tap “Add” to confirm
Follow these steps:
Tap the menu icon (⋮) in the top right
Tap “Add to Home screen”
Tap “Add” to confirm
Follow these steps:
Click the menu icon (⋮) in the top right
Click “Bookmarks”
Click “Bookmark this tab” or press Ctrl+D (Cmd+D on Mac)
Is this tool helpful?
Thanks for your feedback!
How to use the tool
Speed field (v): Enter the object’s final velocity in metres per second, e.g. 10.2 m/s or 18.9 m/s.
Time field (t): Input the elapsed time in seconds, such as 2.7 s or 6.1 s.
Press Calculate: The tool returns acceleration in m/s² rounded to three decimals.
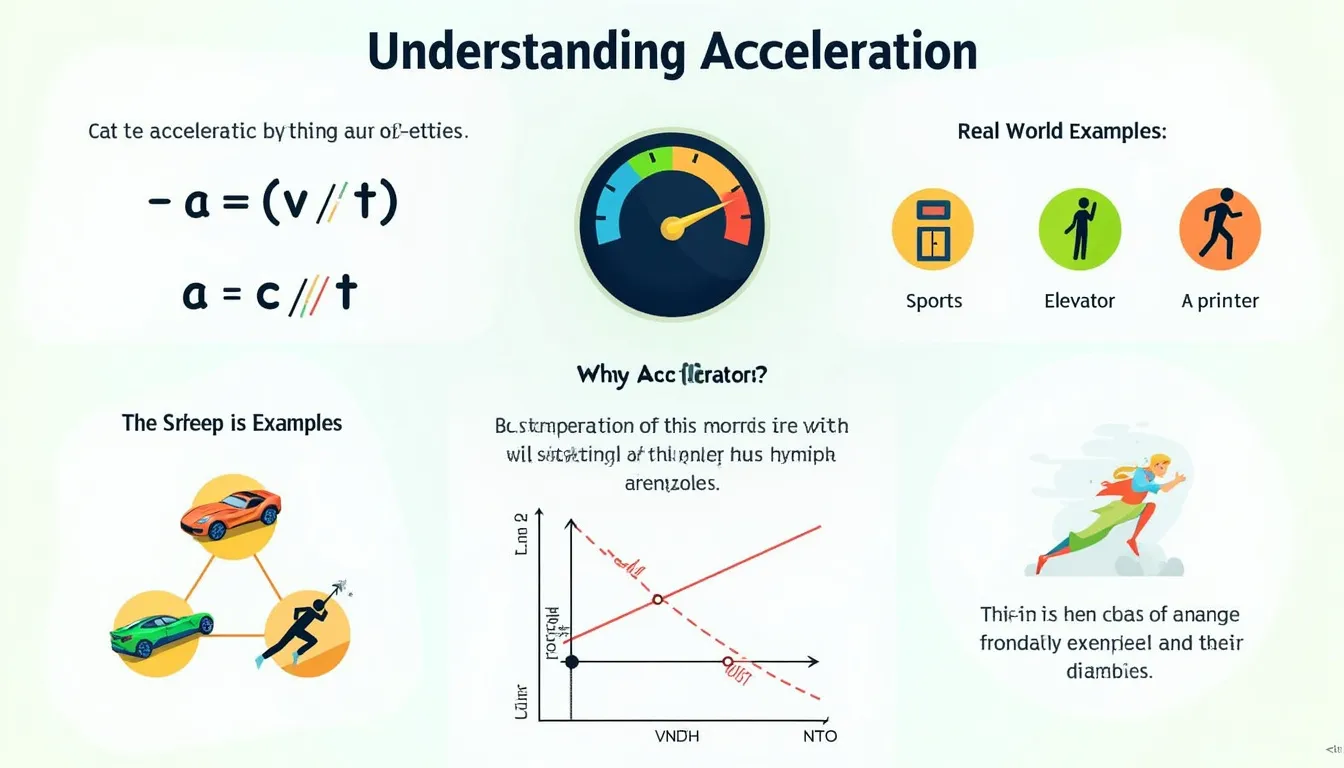
Formula used
Acceleration is final velocity divided by the time taken when initial velocity is zero:
$$a = rac{v}{t}$$
Worked examples
Example A: v = 10.2 m/s, t = 2.7 s ⇒ $$a = rac{10.2}{2.7} = 3.78\ \text{m/s}^2$$
Example B: v = 18.9 m/s, t = 6.1 s ⇒ $$a = rac{18.9}{6.1} = 3.10\ \text{m/s}^2$$
Quick-Facts
Standard gravity: 9.80665 m/s² (BIPM Metrologia, 2019).
ISO 18738 caps elevator acceleration at 1.3 m/s² for comfort (ISO, 2012).
A Formula 1 car can exceed 17 m/s² during launch (FIA Technical Report, 2021).
Human tolerance for brief linear acceleration is ≈5 m/s² (NASA Human Factors, 2021).
FAQ
What is acceleration?
Acceleration is the rate at which velocity changes with time and is a vector quantity (Halliday & Resnick, 2020).
Which unit does the calculator output?
The tool outputs metres per second squared (m/s²), the SI unit for linear acceleration (BIPM SI Brochure, 2019).
Can acceleration be negative?
Yes; a negative value means the object is slowing down or speeding up in the opposite direction (Serway, 2023).
Why must time be greater than zero?
Division by zero is undefined, so t > 0 ensures a meaningful, finite acceleration result (Stewart Calculus, 2021).
How accurate is the calculation?
The tool uses floating-point arithmetic and rounds to 0.001 m/s²; rounding is the only introduced error (IEEE 754 Std., 2019).
Does the tool handle vector components?
No; it assumes straight-line motion with initial velocity of zero. Vector analysis needs separate x, y, z inputs (Giancoli, 2020).
How do I compare the result to gravity?
Divide your acceleration by 9.80665 m/s² to express it in g-units (BIPM, 2019).
Is there a speed limit for safe human exposure?
Sustained accelerations above 5 m/s² can cause discomfort; astronauts train up to 9 m/s² in short bursts (NASA Human Factors, 2021).
Important Disclaimer
The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors. By using our tools, you acknowledge that you have read, understood, and agreed to this disclaimer. You accept the inherent risks and limitations associated with the use of our tools and services.
