Future Value Factor Calculator
Is this tool helpful?
How to use the tool
- Enter the rate per period (percentage). Example 1: 8 %. Example 2: 1.2 % (monthly).
- Enter the number of periods. Example 1: 10 years. Example 2: 36 months.
- Press “Calculate”. The tool outputs the Future Value Factor (FVF).
- Multiply your present amount by the FVF to find its future value.
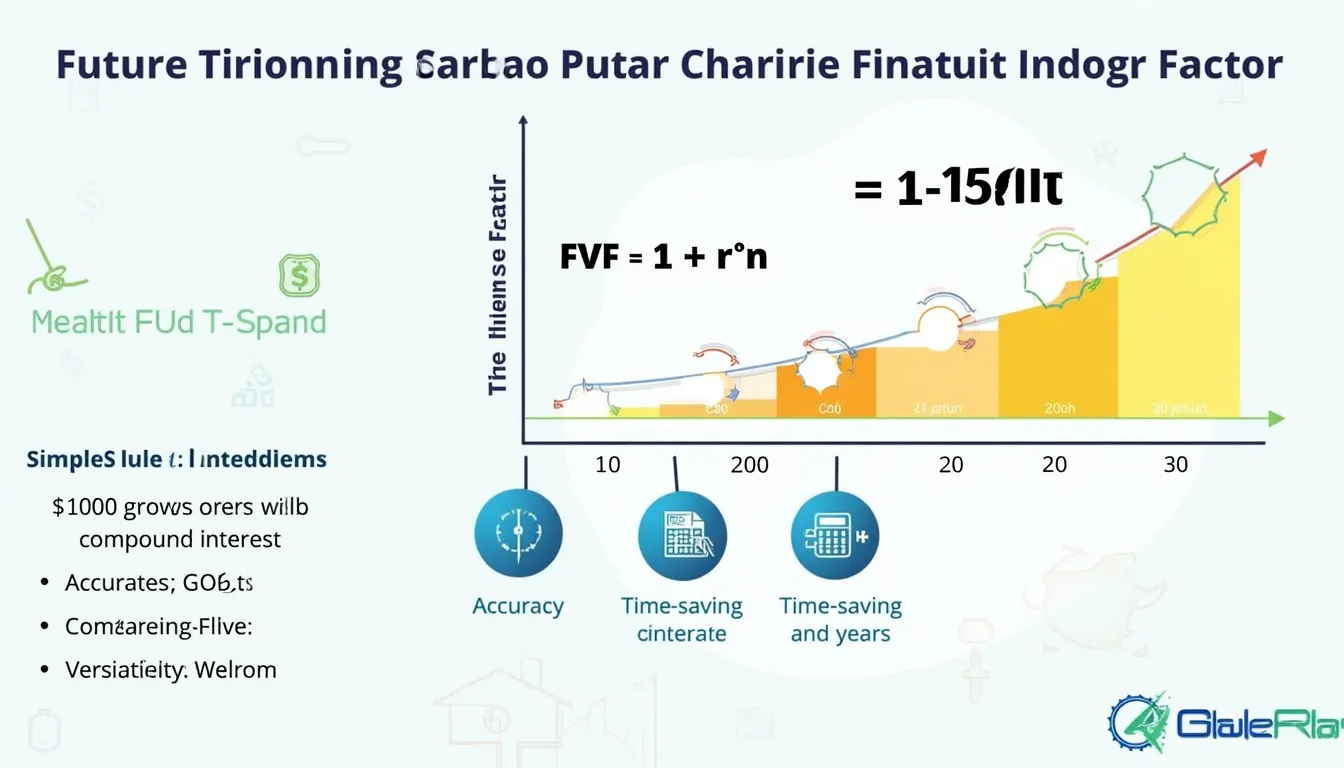
Formula
The calculator applies compound interest with
$$FVF = (1 + rac{r}{100})^{n}$$
- r = rate per period (%).
- n = number of periods.
Example calculations
Example 1: Annual compounding
r = 8 %, n = 10
$$FVF = (1 + 0.08)^{10} = 2.1589$$
$1 today grows to about $2.16 after 10 years.
Example 2: Monthly compounding
r = 1.2 %, n = 36
$$FVF = (1 + 0.012)^{36} = 1.5360$$
$1 today grows to about $1.54 after 36 months.
Quick-Facts
- Core formula: FVF = (1 + r)n (Investopedia, https://www.investopedia.com/terms/f/futurevalue.asp)
- Average U.S. stock return: ≈10 % per year from 1926-2022 (Damodaran, 2023)
- Fed funds rate range: 0 %-5.5 % between 2008-2023 (FederalReserve.gov, 2023)
- Compound interest definition: “Interest earned on both the money you save and the interest you earn” (SEC Investor.gov)
FAQ
What is the Future Value Factor?
The Future Value Factor is a multiplier that converts any present amount to its future value using compound interest (Investopedia, https://www.investopedia.com/terms/f/futurevalue.asp).
How does the calculator work?
You supply rate and periods; it applies $$FVF=(1+r)^n$$ and displays the factor instantly. No other inputs are required.
Can I use quarterly rates?
Yes. Enter the quarterly rate (e.g., 1.5 %) and the number of quarters; the formula remains valid (Corporate Finance Institute, 2023).
Does the tool handle negative rates?
Yes. A negative r yields an FVF below 1, modelling value erosion (European Central Bank, 2022).
Is compound interest always better than simple interest?
Compound interest grows faster because it “earns interest on interest” (SEC Investor.gov), while simple interest does not.
How accurate are the results?
Results are exact to four decimals, limited only by your rate and period precision.
What limits should I use for periods?
For personal finance, 1-600 periods covers months up to 50 years; beyond that, projections risk higher uncertainty (FINRA, 2023).
Why does inflation matter?
Subtract expected inflation to get a real rate; otherwise, the FVF overstates purchasing power (Bureau of Labor Statistics, 2023).
Important Disclaimer
The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. Do not enter personal data, sensitive information, or personally identifiable information in our web forms or tools. Such data entry violates our terms of service and may result in unauthorized disclosure to third parties. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors.