Hypotenuse Calculator: Find Triangle Side Length with Ease | Free Online Tool

How to Use the Hypotenuse Calculator Effectively

Our Hypotenuse Calculator is designed to make finding the hypotenuse length of a right-angled triangle quick and straightforward. Follow these simple steps to use the tool effectively:

1. Enter Side A: Input the length of one side adjacent to the right angle. For example, enter 5.5 or 7.2 depending on your measurement.
2. Enter Side B: Input the length of the other side adjacent to the right angle, such as 6 or 9.3.
3. Select Unit of Measurement: Choose the appropriate unit for your inputs from the dropdown. Options include millimeters (mm), centimeters (cm), meters (m), kilometers (km), inches (in), feet (ft), yards (yd), and miles (mi). Ensure you pick the unit that matches your measurements.
4. Calculate the Hypotenuse: Click the button to compute the hypotenuse length based on your inputs.
5. View Results: The calculator will display the hypotenuse length along with a clear visual representation of the triangle, helping you better understand the relationship between the sides.

Make sure to enter positive numeric values since negative or zero values do not apply for side lengths. If invalid inputs are entered, the calculator will prompt you to correct them.

Introducing the Hypotenuse Calculator: Definition, Purpose & Benefits

The Hypotenuse Calculator is a handy online tool built on the foundational Pythagorean theorem, which enables quick and accurate calculation of the hypotenuse length — the longest side of a right-angled triangle. This calculator simplifies geometric calculations for students, professionals, and DIY enthusiasts alike.

What Is the Hypotenuse?

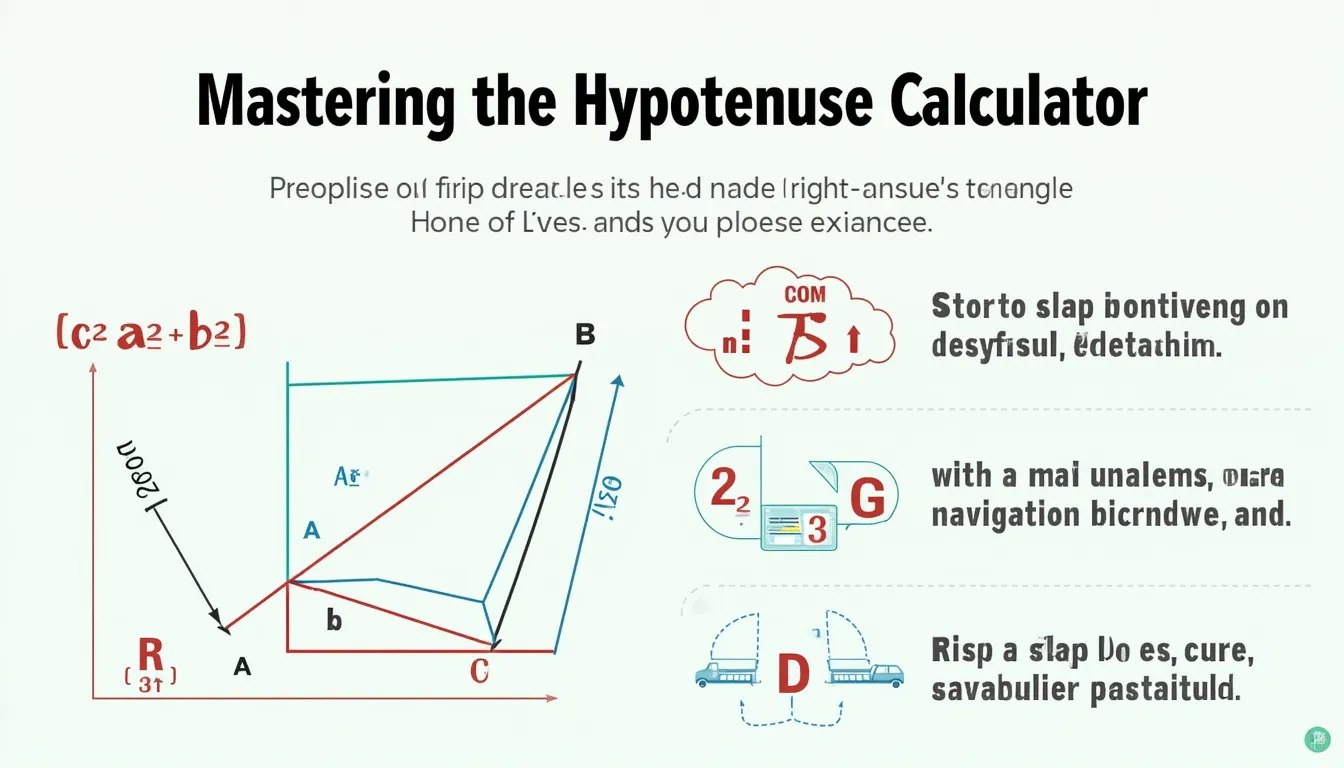
In any right-angled triangle, the hypotenuse is the side opposite the 90-degree angle, and it is always the triangle’s longest side. According to the Pythagorean theorem, the relationship between the sides is expressed as:

$$c^2 = a^2 + b^2$$

• c: The length of the hypotenuse (the calculated side)
• a and b: Lengths of the two sides adjacent to the right angle

Purpose of the Hypotenuse Calculator

This calculator’s core function is to automate the process of finding the hypotenuse without the need for manual computations. It provides:

• Fast calculations: Get immediate results after inputting side lengths.
• Accuracy: Minimizes human error, ensuring precise answers.
• Multi-unit support: Work comfortably using metric or imperial units.
• Visual understanding: Triangle visuals help users comprehend geometric relationships.
• Educational assistance: Ideal for reinforcing the concepts of trigonometry and geometry.

Benefits of Using the Hypotenuse Calculator

1. Time efficiency: Eliminates tedious, manual calculations.
2. Enhanced precision: Delivers rounded results accurate to two decimal places.
3. Wide applicability: Suitable for various fields, from education to engineering.
4. Interactive graphics: Helps users visualize the triangle and its sides.
5. User-friendly: Simple interface that requires no advanced math skills.
6. Online convenience: Accessible anytime, anywhere with internet access.

Example Calculations Using the Hypotenuse Calculator

Example 1: Calculating the Ladder Length

Suppose you need to find the length of a ladder that reaches 3.6 meters high on a wall, with the base placed 2.8 meters away from the wall.

• Side A (base distance): 2.8 meters
• Side B (height): 3.6 meters
• Unit: meters (m)

Enter the values and calculate:

1. Input 2.8 for Side A.
2. Input 3.6 for Side B.
3. Select meters as the unit.
4. Click “Calculate Hypotenuse.”

Result: The ladder length (hypotenuse) is approximately 4.53 meters.

Example 2: TV Screen Diagonal Measurement

If you want to find the diagonal size of a television screen that is 102 inches wide and 58 inches tall:

• Side A (width): 102 inches
• Side B (height): 58 inches
• Unit: inches (in)

Steps to calculate:

1. Input 102 for Side A.
2. Input 58 for Side B.
3. Select inches as the unit.
4. Press the calculate button.

Result: The diagonal screen size (hypotenuse) is about 117.57 inches.

Practical Applications of the Hypotenuse Calculator Across Various Fields

The Hypotenuse Calculator is invaluable in many real-world contexts, enhancing precision and efficiency in measurements:

1. Architecture and Construction

• Roof design: Calculating rafter lengths to determine pitch.
• Structural bracing: Planning diagonal supports in frameworks.
• Site surveying: Finding indirect distances for property layout.

2. Education and Learning

• Geometry learning: Visualizing the Pythagorean theorem in practice.
• Homework help: Checking triangle side calculations easily.
• Math demonstrations: Showing practical triangle applications.

3. DIY and Home Improvement

• Staircase building: Measuring stringers and diagonal lengths.
• Tile cutting: Determining diagonal cuts for correct fitting.
• Landscape planning: Mapping diagonal paths and garden features.

4. Engineering and Manufacturing

• Machine components: Designing precise diagonal parts.
• Packaging: Calculating diagonal dimensions for boxes.
• Antenna installation: Measuring cable lengths at angles.

5. Sports and Navigation

• Sports field layout: Verifying diagonal court measurements.
• Marine and land navigation: Estimating distance in triangular plots.
• GPS triangulation: Calculating positions based on triangular distance.