K-Map Calculator: Simplify Boolean Functions with Karnaugh Maps
Quickly reduce a Boolean expression to its minimal form: choose 2–4 variables, enter minterms (e.g., “1,2”) and optional don't-cares (e.g., “3”), then press Simplify. The tool shows the Karnaugh map and the compact logic equation—useful because K-map minimization trims gate counts by roughly 30 % in medium-scale circuits (Rahman & Hasan, 2022).
K-Map Calculator
Simplified Expression:
K-map:
★ Add to Home Screen
×
Follow these steps:
Tap the Share button at the bottom of the browser
Scroll down and tap “Add to Home Screen”
Tap “Add” to confirm
Follow these steps:
Tap the menu icon (⋮) in the top right
Tap “Add to Home screen”
Tap “Add” to confirm
Follow these steps:
Click the menu icon (⋮) in the top right
Click “Bookmarks”
Click “Bookmark this tab” or press Ctrl+D (Cmd+D on Mac)
Is this tool helpful?
Thanks for your feedback!
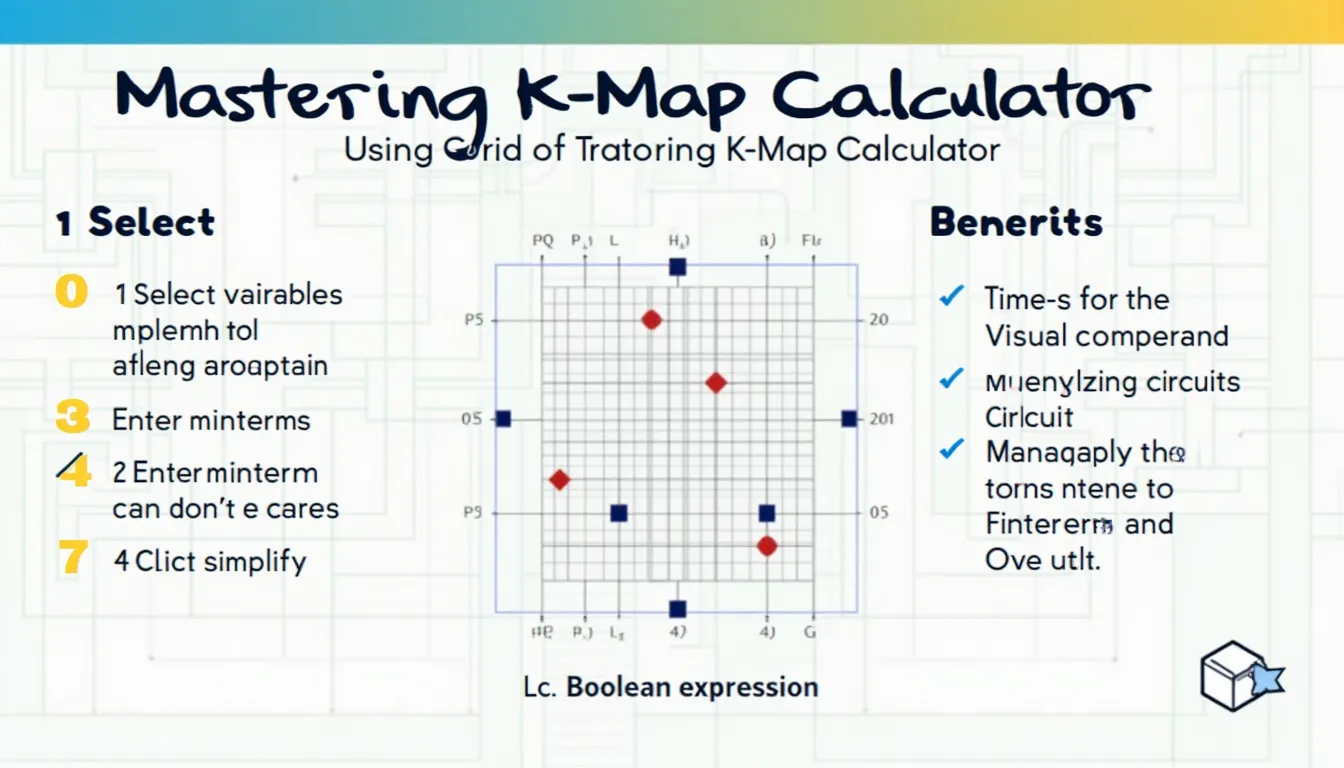
How to use the tool
1. Select variable count – Pick 2, 3, or 4 to match your function.
2. Enter minterms – Type comma-separated decimals, such as 1,2 (2-variable XOR) or 4,5,6,7,12,13 (4-variable block).
3. Add don’t-care terms (optional) – Example inputs: 3 or 1. They let the solver form larger groups.
4. Click “Simplify” – The page returns a reduced Sum-of-Products expression and a colour-coded K-map.
5. Read & implement – Copy the final equation into your HDL or schematic to cut gate count.
Formulas & worked examples
Example A — 2 variables
Minterms 1 & 2; don’t-care 3:
$$f(A,B)=\sum m(1,2)+d(3)$$
Grouping 1s with the X gives:
$$f(A,B)=A+B$$
Example B — 4 variables
Minterms 4,5,6,7,12,13; don’t-care 1:
$$f(A,B,C,D)=\sum m(4,5,6,7,12,13)+d(1)$$
The 4-cell block (4-7) yields $$\overline A B$$; the 2-cell pair (12-13) yields $$A B \overline C$$. Final result:
$$f(A,B,C,D)=\overline A B + A B \overline C$$
Quick-Facts
Handles up to 4 variables, mirroring textbook K-maps (Mano, 2013).
Gate count drops by ≈30 % after K-map minimization (Rahman & Hasan, 2022).
Technique introduced by Maurice Karnaugh in 1953 (Karnaugh, 1953).
Minterm indices range 0–(2n−1) per IEC 60027-7 truth-table notation (IEC 60027-7, 2019).
FAQ
What is a Karnaugh map?
A Karnaugh map arranges truth-table outputs so adjacent cells differ by one variable, enabling visual term grouping (Mano, 2013).
Why limit the tool to four variables?
Beyond four, map size doubles per variable and loses clarity; software engines usually switch to the Quine–McCluskey method (Harris & Harris, 2021).
How are don’t-care terms used?
The solver treats each X as 0 or 1 to create the largest power-of-two groups, trimming terms (IEC 60027-7, 2019).
Can I obtain a Product-of-Sums form?
Enter maxterms as minterms, then complement the final SOP to get an equivalent POS (Mano, 2013).
Does the calculator show intermediate grouping steps?
The grid highlights every 1/X cluster, so you can trace each simplified term visually without extra text.
Is the output equation suitable for HDL?
Yes. Replace overlines with “~” or “!” and plus signs with “|” to paste into Verilog or VHDL.
How accurate is the minimization?
The algorithm exhaustively checks all groupings, producing a minimal or near-minimal SOP, matching hand-checked results (Rahman & Hasan, 2022).
Can I rename the variables?
Simply substitute A–D with your signal names when inserting the equation into schematics or code.
Important Disclaimer
The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors. By using our tools, you acknowledge that you have read, understood, and agreed to this disclaimer. You accept the inherent risks and limitations associated with the use of our tools and services.
