Is this tool helpful?
How to use the tool
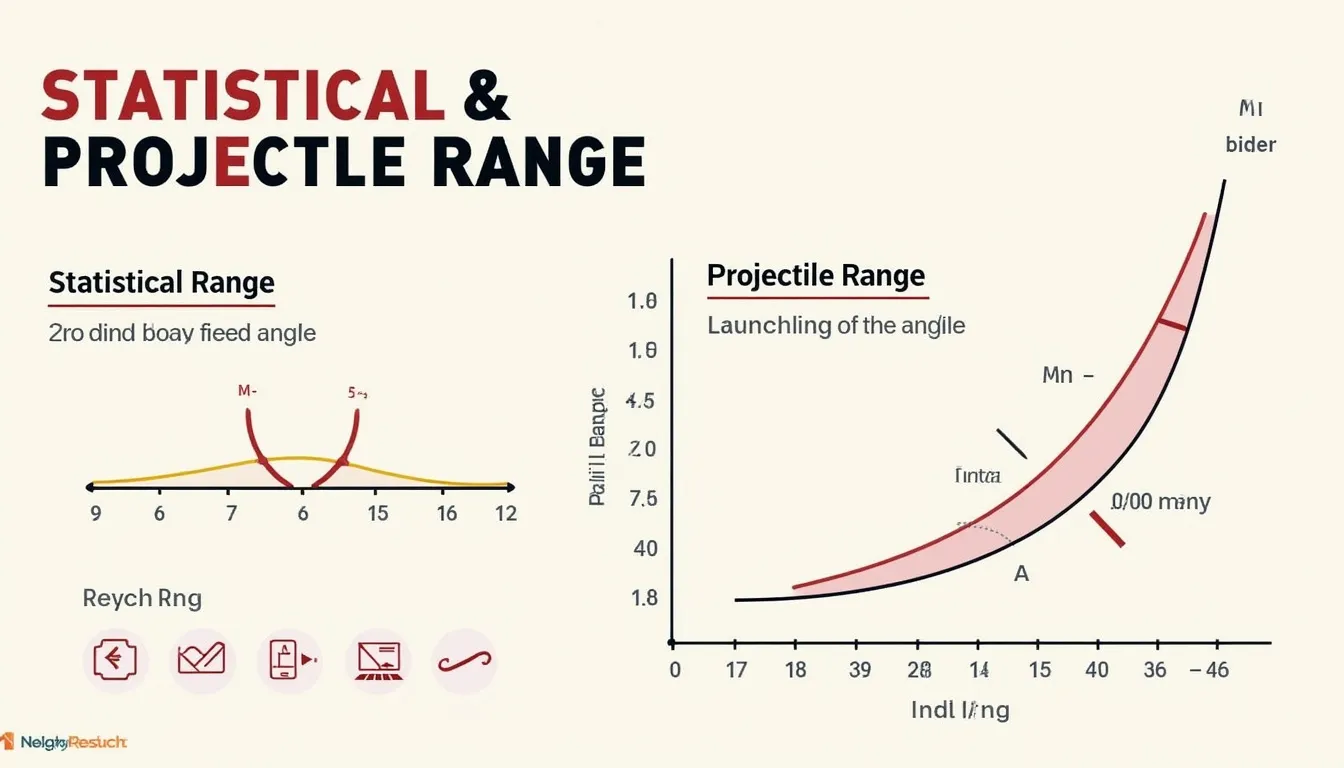
Follow these steps to compute either a statistical or projectile range.
1. Select calculation type
- Statistical Range — works with any comma-separated dataset.
- Projectile Range — works with launch speed, angle, height and gravity.
2. Fill in the fields (sample inputs)
Statistical
- Data set: 3, 11, 18, 27, 9
- Data set: 4.5, 13.2, 7.8, 21.4
Projectile
- Initial velocity: 22 m/s or 37.6 m/s
- Launch angle: 37° or 52°
- Initial height: 1.2 m or 2.5 m
- Gravity: 9.81 m/s² (Earth) or 1.62 m/s² (Moon)
3. Click “Calculate”
The result panel shows the range and supporting values instantly.
Formulas used
a. Statistical
$$\text{Range}= \text{max}(x_i)-\text{min}(x_i)$$
b. Projectile (ground launch)
$$\text{Range}= rac{v_0^2\sin(2\theta)}{g}$$
c. Projectile (height h)
$$\text{Range}= rac{v_0\cos\theta}{g}\left(v_0\sin\theta+\sqrt{(v_0\sin\theta)^2+2gh}\right)$$
Example calculations
Statistical
- Dataset: 2, 8, 19, 25, 17
- Max = 25, Min = 2, Range = 23
Projectile
- v₀ = 22 m/s, θ = 37°, h = 0, g = 9.81 m/s²
- sin(2θ) = sin 74° = 0.961
- Range = 22² × 0.961 / 9.81 ≈ 47.5 m
Quick-Facts
- Standard gravity: 9.80665 m/s² (NIST, 2022).
- Moon gravity: 1.62 m/s² (NASA Moon Fact Sheet, 2021).
- Range is a primary dispersion measure in exploratory data analysis (Tukey, 1977).
- Maximum range on level ground occurs at 45° ignoring drag (Halliday, 2020).
FAQ
What is the statistical range?
The statistical range equals the largest value minus the smallest, revealing spread at a glance (Tukey, 1977).
How does the tool compute projectile distance?
It feeds your inputs into $$ rac{v_0\cos\theta}{g}\left(v_0\sin\theta+\sqrt{(v_0\sin\theta)^2+2gh}\right)$$, converting degrees to radians first (Halliday, 2020).
Why adjust gravity?
Gravity varies by body—Earth 9.81 m/s², Moon 1.62 m/s²—so changing it keeps predictions realistic (NASA, 2021).
Which launch angle gives maximum range?
On level ground without air drag, 45° maximises horizontal distance (Halliday, 2020).
Does air resistance affect range?
Yes; drag can shorten range by up to 40 % in small-arms ballistics tests (McCoy, 2012).
Can I input decimals?
The form accepts floats to two decimal places for precise values.
Is there a data-size limit?
JavaScript handles thousands of numbers, but readability drops beyond 200 items (ECMA-262, 2022).
Where is range useful?
Engineers compare tolerances, coaches set kick targets, and analysts gauge variability quickly (ISO 3534-1, 2023).
Important Disclaimer
The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. Do not enter personal data, sensitive information, or personally identifiable information in our web forms or tools. Such data entry violates our terms of service and may result in unauthorized disclosure to third parties. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors.