Z-Score Calculator: Measure Data Point Deviation from Mean Easily
A z-score shows how far a value sits from the mean in standard deviations; about 95 % of normally distributed values lie between −1.96 and +1.96 z (Altman & Bland, 1995 https://www.bmj.com/content/310/6976/298).
Z-Score Calculator
Results:
★ Add to Home Screen
×
Follow these steps:
Tap the Share button at the bottom of the browser
Scroll down and tap “Add to Home Screen”
Tap “Add” to confirm
Follow these steps:
Tap the menu icon (⋮) in the top right
Tap “Add to Home screen”
Tap “Add” to confirm
Follow these steps:
Click the menu icon (⋮) in the top right
Click “Bookmarks”
Click “Bookmark this tab” or press Ctrl+D (Cmd+D on Mac)
Is this tool helpful?
Thanks for your feedback!
How to use the tool
Data Point (x) – type the value you want to standardise. Example A: 120 kg; Example B: 72 ms.
Mean (μ) – enter your dataset’s average. Example A: 100 kg; Example B: 80 ms.
Standard Deviation (σ) – supply the positive spread measure. Example A: 15 kg; Example B: 8 ms.
Decimal Places – pick 2-4 decimals for the result.
Press “Calculate” – the script returns the z-score plus a plain-English interpretation.
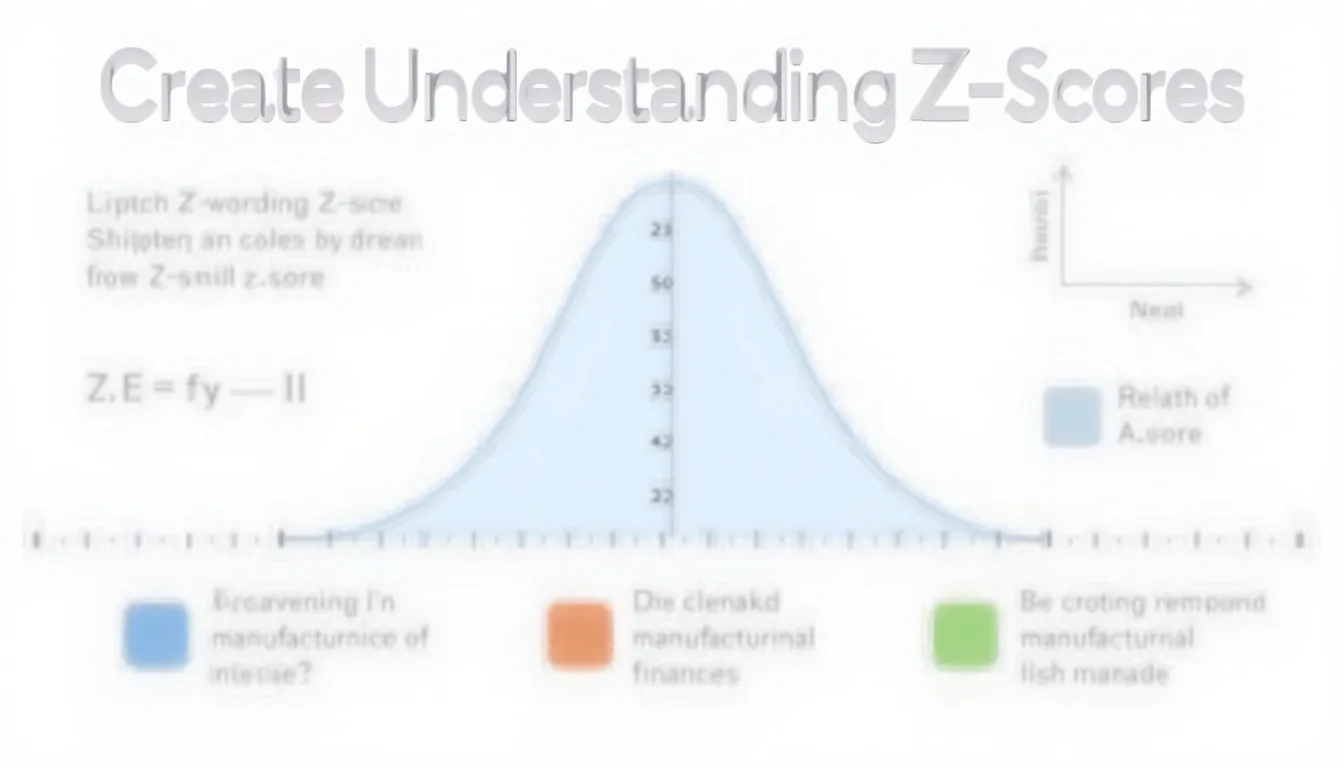
Formula
$$Z = rac{x – \mu}{\sigma}$$
Worked examples
Example A: $$Z = rac{120-100}{15}=1.33$$ – 1.33 σ above the mean.
Example B: $$Z = rac{72-80}{8}=-1.00$$ – 1 σ below the mean.
Quick-Facts
Standard normal distribution has μ = 0, σ = 1 (NIST e-Handbook, 2012 https://itl.nist.gov/div898/handbook/).
±1.96 z captures 95 % of data (Altman & Bland, 1995 https://www.bmj.com/content/310/6976/298).
Values beyond ±3 z are classed as outliers (ISO 13528:2015).
σ must be > 0 for the formula to hold (DeGroot & Schervish, 2012).
The calculator rounds to up to 4 decimals for precision.
FAQs
What is a z-score?
A z-score expresses how many standard deviations a value lies above or below the mean, enabling comparison across different units (NIST, 2012 https://itl.nist.gov/div898/handbook/).
How does the calculator work?
It subtracts the mean from your data point, divides by the standard deviation, then rounds to your chosen decimals—all in your browser, so no data leave your device.
Why use z-scores instead of raw values?
Z-scores standardise data, letting you compare exam marks with blood-pressure readings on the same statistical scale (Montgomery, 2019 https://www.wiley.com/en-us/Introduction+to+Statistical+Quality+Control).
What does a negative z-score tell me?
The value sits below the mean; for example, z = −1 means it is one standard deviation lower (NIST, 2012 https://itl.nist.gov/div898/handbook/).
When is a z-score unreliable?
If your dataset is heavily skewed or has thick tails, the normality assumption fails, reducing interpretive power (West et al., 2014 https://doi.org/10.1037/met0000028).
How precise should I make my result?
Two decimals suit most reports; choose four when scientific standards demand higher accuracy (ISO 3534-2:2006).
Can I convert z-scores to percentiles?
Yes—use standard normal tables; e.g., z = 1.00 corresponds to the 84th percentile (McClave & Sincich, 2020 https://www.pearson.com).
Is the calculation different for sample data?
No; you still use the same formula, but compute σ from sample data with n − 1 in the denominator to get an unbiased estimate (Walpole et al., 2017).
Important Disclaimer
The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. Do not enter personal data, sensitive information, or personally identifiable information in our web forms or tools. Such data entry violates our terms of service and may result in unauthorized disclosure to third parties. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors.
